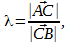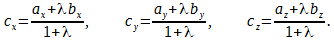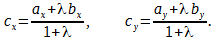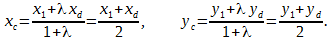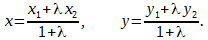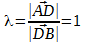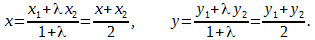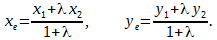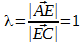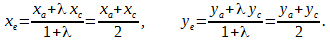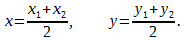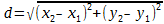деление отрезка в заданном отношении векторы
Лекция Способы задания векторов. Деление отрезка в заданном отношении. Скалярное произведение двух векторов и его основные свойства.
1.4. Способы задания векторов
Вектор может быть задан следующими способами:
1. Координатами вектора
2 

и конечной 
3. Модулем вектора 

которые он образует с координатными осями.
При этом значения 

Между этими способами задания 
векторов существует определённая связь. a x
Например, переход от (2) к (1) x a y
осуществляется следующим образом :
т 


Переход от (3) к (1) и наоборот
о


1.5. Деление отрезка в заданном отношении
Р 




Построим векторы : 
Из условия коллинеарности векторов



Полученное равенство представим в
координатной форме х Оу

Замечание 1. Из формул (1) следует частный случай деления отрезка пополам 
Известно, что центр тяжести треугольника
лежит на пересечении его медиан и, если
свойству медиан 
Определим вначале координаты х С
точки К :
далее по формулам (1) получим координаты точки М :
Тема 2: Скалярное произведение
2.1. Скалярное произведение двух векторов и его основные свойства
Определение. Скалярным произведением двух векторов 


Замечание 2. Формулу (2) можно представить в другой форме


Рассмотрим механический смысл скалярного произведения. Если 



Из определения скалярного произведения следуют его свойства:
1. 
2. 


3.
Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:
4.
Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.
2.2. Скалярное произведение векторов, заданных координатами
Из определения и свойства (1) скалярного произведения следуют формулы : 
Аналогично получаем :

2.3. Длина вектора. Угол между двумя векторами.
По формулам (2) и (4) получаем

Из определения скалярного произведения и формул (4), (5) следует



Если в формуле (7) положить 

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов


Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.
Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство
Пример 2. Даны два вектора 
По формулам (5) и (7) получаем
Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору 

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора 
Из второго уравнения системы получаем 


Из этого уравнения 


Деление отрезка в данном отношении, координаты, примеры, решения.
В этой статье мы разберемся с нахождением координат точки, которая делит некоторый отрезок в заданном отношении. Сначала мы получим формулы для нахождения координат такой точки по координатам концов отрезка. После этого приведем подробные решения нескольких характерных примеров.
Навигация по странице.
Вывод формул для нахождения координат точки, делящей отрезок в данном отношении, на плоскости.
Начнем с постановки задачи на плоскости.
Поставленная задача может быть решена с помощью векторов.
В силу операции сложения векторов можно записать равенства 

Так как точка С делит отрезок АВ в соотношении 











Осталось вычислить координаты вектора 






Координаты точки, которая делит отрезок в заданном отношении, в пространстве.
Теперь рассмотрим задачу нахождения координат точки, делящей отрезок в данном отношении, не на плоскости, а в трехмерном пространстве.
Нахождение координат точки, делящей отрезок в данном отношении, примеры и решения.
Пришло время применить полученные формулы при нахождении координат точки, делящей отрезок в заданном отношении. Рассмотрим решения наиболее часто встречающихся задач по этой теме.

В данном примере 





Одной из самых характерных задач, в которой приходится вычислять координаты точки, делящей отрезок в заданном соотношении, является задача на нахождение центра тяжести треугольника.
Осталось вычислить искомые координаты центра тяжести треугольника:

Деление векторов в данном соотношении
Пусть вектор 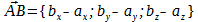
пусть при этом известно соотношение длин векторов
тогда координаты точки C(cx; cy; cz) находятся по формулам
Примеры решения заданий по делению векторов и отрезков
Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.
Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении
Подставим в последнее равенство координаты xc, yc, xd, yd:
3 = (x1 + 5)/2, 4 = (y1 + 6)/2,
откуда находим, x1 = 1, y1 = 2. Точка A имеет координаты A(1, 2).
Поскольку точка D есть середина отрезка CB, то xd = (xc + x2)/2, или 5 = (3 + x2)/2, отсюда x2 = 7.
отсюда y2 = 8. Получили B(7, 8).
О т в е т: A(1, 2), B(7, 8).
Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:
Поскольку отрезки делятся на равные части, то
Тогда формула приобретает вид:
Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.
Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.
Назовём точку пересечения диагоналей точкой E.
Поскольку этой точкой диагонали делятся на два равных отрезка
то формула приобретает вид:
Найдём середину отрезка AC:
Итак, точка E имеет координаты (0, 0).
Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда
подставим известные значения:
Теперь найдём вторую координату:
подставим известные значения:
Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:
Точка D имеет координаты (-1, 2).
Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:
О т в е т: Длина медианы, проведённой из вершины B, равна 13.