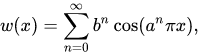Точка это то часть чего есть ничто

Точка это то часть чего есть ничто

Трудно переоценить значение книги Евклида «Начала». В качестве учебника при школьном преподавании математики (особенно геометрии) эту книгу использовали вплоть до XX в. Идеи, высказанные в «Началах», на протяжении более чем двух тысячелетий оказывали стимулирующее воздействие на новые математические исследования. Классическая механика, лежащая в основе естествознания XVII–XIX вв., описывает мир как находящийся в абсолютном пространстве, устроенном по законам геометрии Евклида. Осуществленная в «Началах» попытка логического выведения целостной теории из ограниченного числа первоначальных положений вызвала многочисленные подражания: в их числе – основополагающая для классической механики книга И. Ньютона «Математические начала натуральной философии», а также философский трактат Б. Спинозы «Этика, излагаемая геометрическим методом».

«Начала» подводят итог предшествующему развитию греческой математики, объединяя в себе теории, содержавшиеся в не дошедших до нас трактатах Гиппократа Хиосского, Теэтета, Евдокса и др. Последующие математики ссылались на положения «Начал» как на нечто окончательно установленное. В то же время некоторые теории, разработанные ранее, в эту книгу не вошли: по-видимому, автор стремился дать в ней именно «начала», «элементы», на основе которых могут быть развиты все разделы современной ему математики. Хотя основное место в греческой математике, и в «Началах» в том числе, занимает геометрия, эта книга также содержит много важных сведений из греческой арифметики.

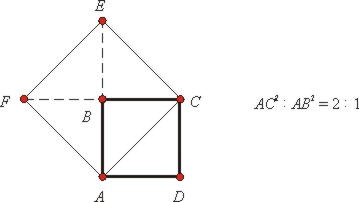
Греческое название книги – «Стойхейя» – исходно обозначало алфавит, а также элементы, в частности, те, из которых состоит мироздание; греки насчитывали четыре элемента – землю, воду, огонь и воздух (рус. «стихия» также происходит от греч. «стойхейя»). Философ-неоплатоник V в. н. э. Прокл в комментариях к «Началам» утверждает, что структура книги отображает устройство космоса: она начинается с самых простых понятий – точки и прямой – чтобы в конце концов придти к учению о правильных многогранниках, которые, согласно философии Платона, лежат в основе структуры мира (четыре элемента имеют формы четырех из пяти правильных многогранников, а весь мир в целом – форму пятого, додекаэдра).

Если математические тексты Древнего Востока представляют собой лишь сборники предписаний для решения тех или иных задач, то греческая математика очень рано пришла к осознанию важности доказательств, обоснований одних положений с помощью других, уже установленных ранее. Появился идеал научной системы, в которой, во-первых, используемые термины имели бы четкие определения, а во-вторых, совокупность утверждений логически строго выводилась бы из немногих первоначальных аксиом. Этот идеал со всей ясностью сформулирован в логических трактатах Аристотеля. Первые попытки аксиоматического изложения математики были осуществлены еще до Евклида, но именно его «Начала», по-видимому, стали наиболее совершенным произведением такого рода в античности, полностью затмившим достижения предшественников.

«Начала» состоят из тринадцати книг. Каждая книга начинается с определений используемых терминов; кроме того, в начале первой книги сформулированы аксиомы и постулаты. Далее идут «предложения», доказываемые на основе определений входящих в них терминов, а также на основе аксиом, постулатов и доказанных ранее предложений. Значительную часть предложений составляют задачи на построение циркулем и линейкой. В этих случаях приводятся способ построения и доказательство того, что построенная фигура удовлетворяет условию задачи.

В I книге приводятся аксиомы и постулаты, а затем излагаются основные свойства треугольников, параллелограммов, трапеций. Венчает книгу теорема Пифагора.
Во II книге излагаются основы геометрической алгебры.

III книга посвящена свойствам круга, его касательных и хорд.
В IV книге строятся правильные треугольник, четырехугольник, пятиугольник, десятиугольник. Изящное построение правильного пятнадцатиугольника, которым заканчивается книга, возможно, принадлежит самому Евклиду.
Книга V содержит общую теорию отношений величин.
В VI книге Евклид излагает учение о подобии и применяет его к решению геометрических задач, эквивалентных квадратным уравнениям.
Книги VII–IX посвящены арифметике – теории целых чисел и их отношений (т. е., фактически, рациональных чисел). Здесь рассматриваются свойства операций с такими числами и проблемы делимости, вводится алгоритм Евклида для поиска наибольшего общего делителя двух чисел, доказывается, что простых чисел бесконечно много.
Книга X, считающаяся одной из самых сложных, излагает классификацию квадратичных иррациональностей.
Книги XI–XIII посвящены стереометрии. Книга XI содержит основные факты о прямых и плоскостях в трехмерном пространстве, а также об объемах параллелепипедов и призм.
В книге XII с помощью довольно тонкой техники (т. н. метода исчерпывания) доказывается, что площади кругов пропорциональны квадратам их диаметров, а объемы шаров – кубам их диаметров.
В книге XIII излагается учение о правильных многогранниках.
Впоследствии к тексту Евклида начали присоединять еще книги XIV–XV, также посвященные правильным многогранникам. Книгу XIV написал математик Гипсикл (II в. до н. э.), книга XV составлена в школе Исидора Милетского (VI в. н. э.).

Аристотель справедливо отмечал, что нельзя определить все термины: определяя одни термины на основе других, мы в конце концов придем к первичным, неопределяемым терминам. В современных аксиоматических изложениях геометрии в качестве неопределяемых терминов обычно рассматриваются точка, прямая, плоскость и некоторые другие. Евклид, однако, стремился определить и эти термины тоже, например:

Историки математики расходятся в мнениях, что именно имел в виду Евклид, давая эти определения. В любом случае такие определения имеют целью скорее описание определяемых объектов, которое должно отсылать к интуитивно ясному образу точки, прямой и т. д. Ввиду их расплывчатости такие определения не используются в доказательствах.

Определения, используемые в доказательствах – это, например, такие:

В идеальном случае все термины, встречающиеся в определениях, должны быть определены ранее либо принадлежать к узкому кругу неопределяемых терминов. В действительности Евклид определяет такие термины, как «круг», «окружность», «диаметр», «прямой угол», «треугольник», но не определяет понятий «содержащаяся между», «отсекаемая», «встречается», «пересекает» и т. д. Значения всех этих слов, по-видимому, должны быть ясны интуитивно, из обычного словоупотребления.

Источник

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Определения Евклида

Первую Книгу “Начал” открывают многочисленные определения, за которыми следуют пять знаменитых постулатов. Далее, перед тем как Евклид начинает доказывать теоремы, он приводит список общих понятий. Первые несколько определений следующие:

Определение 1.1. Точка — это то, часть чего есть ничто.

Определение 1.2. Линия — это длина без ширины.

Определение 1.3. Концы линий — это точки.

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней.

Постулаты — это конструкции следующего вида:

Можно нарисовать прямую линию, соединяющую одну точку с любой другой.

Общие понятия — это аксиомы, такие как:

Объекты, равные одному и тому же объекту, равны между собой.

Следует отметить определенные моменты.

1. Евклид, кажется, определяет точки два раза (определения 1 и 3) и линией два раза (определения 2 и 4). Это довольно странно.

2. Евклид никогда не использует определения и никогда не ссылается на них в остальной части текста.

3. Некоторые понятия он нигде не определяет. Например, отсутствует определение порядка точек на прямой. Поэтому то, что одна точка расположена между двумя другими, также не определено, но, конечно же, это используется.

4. В пятой Книге “Начал” рассматриваются величины и их пропорциональность. Однако Евклид понятие величины не определяет, и современному читателю кажется, что Евклиду не удалось ввести величины с той строгостью, которой он знаменит.

5. Когда Евклид вводит величины и числа, он дает несколько определений, но не постулатов или общих понятий. Например, можно было бы ожидать от Евклида постулирования, что , и т.д., но он этого не делает.

Когда Евклид вводит числа в седьмой Книге, он дает определение, очень похожее на основные определения в начале первой Книги:

Единица — это то, благодаря чему каждая из вещей, которые существуют, называется одной.

Некоторые историки математики предположили, что нет разницы между способами введения основных определений в начале Книги I и в Книге V не потому, что Евклид писал пятую Книгу с меньшей строгостью. Вернее, они предполагают, что Евклид всегда оставлял основные понятия неопределенными, и определения в начале первой Книги являются более поздними добавлениями. Каковы доказательства этого?

Первый комментарий будет по поводу объяснения, почему Евклид никогда не ссылается на основные определения. Если бы их не было в тексте, который написал Евклид то, конечно, он не мог бы сослаться на них. Следующим пунктом следует отметить, что они очень похожи на работу, которая приписывается Герону и называется “Определение понятий геометрии”. Она содержит 133 определения геометрических понятий, начиная с точки, линии и т.д., которые очень близки к данным Евклидом. Кнорр в своей статье (W.R. Knorr, ‘Arithmêtikê stoicheiôsis’ : on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180-192) убедительно доказывает, что эта работа на самом деле принадлежит Диофанту. Дело вот в чем. Основано ли “Определение понятий геометрии” на “Началах” Евклида или основные определения из этой работы были включены в более поздние версии “Начал”?

Мы должны учесть то, что Секст Эмпирик говорит об определениях. Прежде всего заметим, что Секст писал около 200 г. н.э., и до сравнительно недавнего времени считалось, что Герон жил позже этого времени. Если бы это было так, то, конечно, Секст не мог бы сослаться на то, что написал Герон. Однако в последнее время годы жизни Герона отнесли к первому веку нашей эры, и это говорит о том, что Секст писал позже него. Другая часть головоломки, которую мы должны рассмотреть – это более ранние версии “Начал” Евклида, которые можно найти. Когда произошло извержение Везувия в 79 г. н.э., Геркуланум вместе с Помпеей и Стабией был уничтожен. Геркуланум был похоронен под твердой вулканической массой примерно на глубине 16 м и находился там до раскопок города, которые начались в XVIII веке. Особые условия влажности под землей способствовали сохранению дерева, тканей, продуктов питания, и, в частности, папирусов, которые позволили нам узнать важные сведения. Один из найденных папирусов содержит фрагменты “Начал”. Очевидно, что он был написан до 79 г. н.э. Так как Филодем (Philodemus), ученик Зенона Сидонского, пренес туда свою библиотеку папирусов вскоре после 75 г. до н.э., версии “Начал”, вероятно, датируются приблизительно этим временем.

Давайте вернемся к Сексту, который пишет о “математиках, описывающих геометрические объекты”. Интересно, что слово “описание” не используется в “Началах”, но употребляется в “Определении понятий геометрии” Герона. Снова описания, которые он дает, ближе к точным словам Герона, чем к тем, которые можно найти у Евклида. Когда Секст дает определение круга, он использует слово “определение”, которое является словом Евклида. Секст цитирует точное определение круга, которое появляется во фрагменте из Геркуланума. Это не относится к определению окружности, хотя Евклид действительно использует понятие окружности. Более поздние версии “Начал”, которые дошли до нас, включают определение окружности в определение круга.

Ничто из написанного выше не доказывает, что основные определения геометрических объектов были добавлены в “Начала” позже. Достаточно убедительно показано только, что определение круга было расширено за счет того, что в более поздних изданиях книги в него было включено определение окружности. Гипотеза состоит в том, что перед Секстом, когда он пишет, имеются “Начала” и “Определения понятий геометрии”, и он использует слово “описать”, когда он ссылается на Герона, и “определить”, когда ссылается на Евклида. Даже если это верно, то это все равно не доказывает, что версия “Начал”, которая лежит перед Секстом, не содержит основных определений геометрических объектов, но она, по крайней мере, говорит о том, что это стоит обсуждать. Что вы думаете по этому поводу?

И последнее, над чем стоит подумать. Мы привели выше:

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней.

Что это значит? Это описание кажется странным для Евклида, потому что оно выглядит бессмысленным. Сравните это с определением прямой в “Определениях понятий геометрии”:

Прямая линия — это линия, которая одинакова по отношению ко всем точкам на ней, лежит прямо и максимально натянута между своими концами.

Снова вопрос к читателям: вы думаете, что определение, входящее в “Начала”, является искажением определения Герон и было добавлено позже, или вы думаете, что Евклид дал весьма неточное определение, которое было улучшено Героном? Почему бы не использовать определение прямой линии как кратчайшего расстояния между двумя точками?

Источник

Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века

Что такое линия? Чем отличаются разные кривые друг от друга? Эти вопросы математики задают себе уже 2500 лет, и путь к ответам на них не лишен драматизма — открытие иррациональных длин отрезков было, по легенде, трагедией для мировоззрения пифагорейцев, а открытие заполняющих плоскость кривых Пеано в начале ХХ столетия заставило ученых пересмотреть свои представления о непрерывности и размерности пространства. Математик и художник Давид Кац — об истории понятия «кривая» в математике Античности и Средневековья и математическом анализе Нового времени.

Узоры древности

Интерес человека к прямым и искривленным линиям можно отследить с древнейших времен. Самые разные кривые мы видим в геометрических узорах на керамике и в архитектуре. Кроме достаточно простых узоров, составленных из прямых линий, часто можно встретить и что-то более сложное: спирали, волнистые линии и другие.

Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.

Греция: длина без ширины

Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:

Определение 1.1. Точка — это то, часть чего есть ничто.

Определение 1.2. Линия — это длина без ширины.

Определение 1.3. Концы линий — это точки.

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)

Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.

Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):

Прямая линия — это линия, которая одинакова по отношению ко всем точкам на ней, лежит прямо и максимально натянута между своими концами.

Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.

Читайте также

В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.

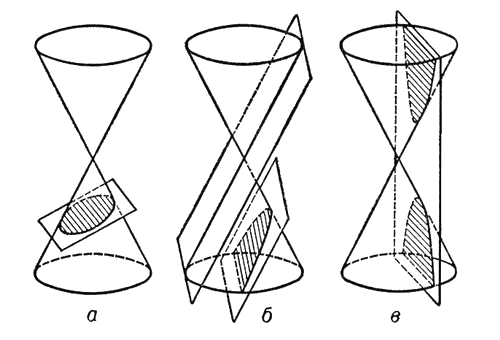
Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.

Приведем и несколько других примеров, известных грекам.

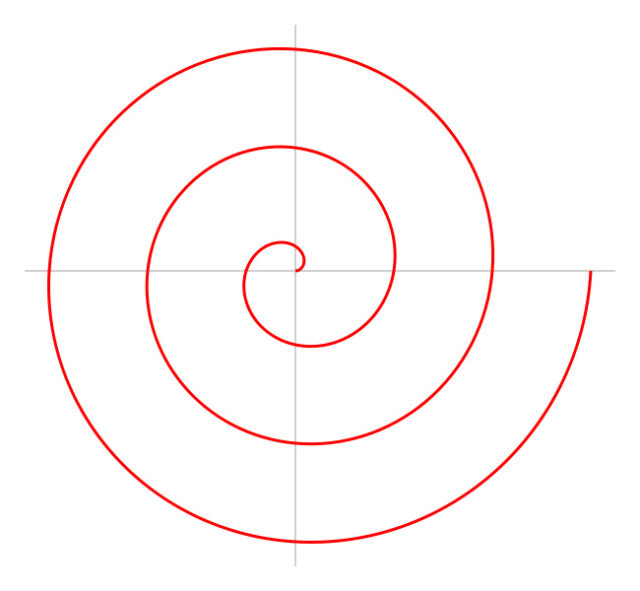
Знаменитая архимедова спираль:

Вторжение иррационального

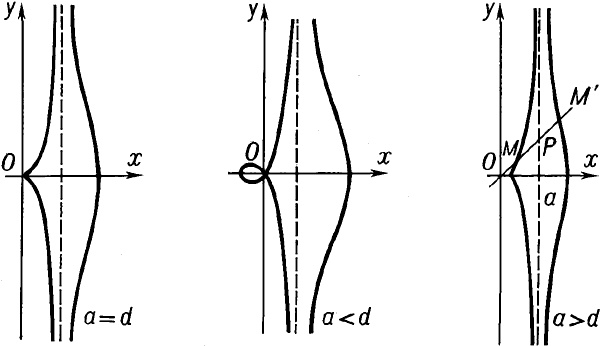
Для пифагорейцев это была печальная новость — в рамках арифметики им такие числа не встречались, поэтому казалось, что и в целом вычисления с длинами оказывались под угрозой.

Интересно, что позже, в рукописи «Выпрямляющий кривое» (в рамках нашей статьи это предельно интригующее название — чуть позже станет понятно почему) некоего Альфонсо, предположительно, крещеного еврея, жившего в Испании между XIII и XV веками, к несоразмерности длин отношение уже гораздо более доброжелательное:

«Следует знать, что от ученых не скрыто то, как поступают люди, которые обвивают прямыми тонкими нитями из шелка, или льна, или другого материала скрепленный круг и измеряют его окружность прямой линией. Однако следует знать, будет ли на самом деле так, как это воспринимается чувством, которое обладает приблизительностью, ибо чувство недостаточно для этого при той приблизительности, которая имеется в нем. Ведь всякие две линии, не равные друг другу, можно разрезать на очень маленькие части так, что чувством будут их воспринимать как равноценные. Вместе с тем возможно, что эти величины несоизмеримы и что видов иррациональной меры бесконечное количество, как это доказано в 10-й книге Евклида».

Координаты и разрывы

Значительное развитие в понимании кривых линий произошло с переходом от геометрического описания к алгебраическому — в частности, к описанию кривых через уравнения.

В действительности нечто похожее на уравнение встречается у Архимеда и Аполлония Пергского — это так называемые симптомы конических сечений.

Затем координаты (в виде заимствованных из географии понятий долготы и широты) встречаются у Николая Орезмского во второй половине XIV столетия. В XVI веке Виет начал использовать символы для записи уравнений. И, наконец, Рене Декарт (синхронно с ним — Пьер де Ферма) развил идеи, совмещающие символьную запись уравнений и систему координат. Его труд пользовался огромной популярностью и быстро получил широкое распространение и существенное развитие. В системе координат появились отрицательные значения, саму сетку координат научились строить косоугольной.

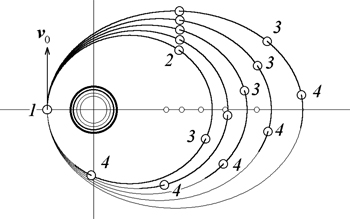
Этот подход, хотя и ограниченно, применял Ньютон. Впоследствии Кеплер для представления траекторий движения планет активно использовал конические сечения в координатах, геометрически описанные еще греками.

Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.

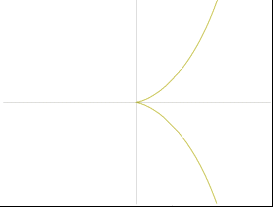
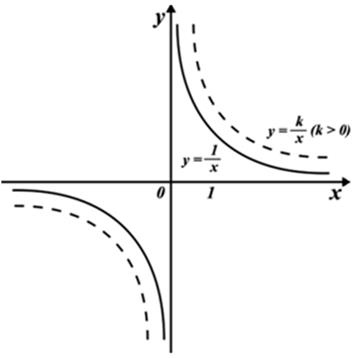
Интересно, что уже на этом, алгебраическом уровне возникают кривые с любопытными особенностями. Возьмем, например, известную многим со школы гиперболу — график функции 1/x. Его можно построить по точкам, но несложно сообразить, что уравнение y = 1/x имеет решение для любого x, кроме одного: x = 0 (на ноль делить нельзя). Это сказывается и на графике:

Что происходит в окрестности нуля? Нетрудно ответить. Давайте подойдем к нему справа. Когда мы подставляем в качестве x в выражение 1/x целое число больше 1, мы получаем дробь. Чем больше число, тем меньше получается дробь — этим и объясняется то, что график идет всё ниже и ниже по мере продвижения вправо. Подставляем х = 100, получаем у = 1/100, подставляет 1000000, получаем 1/1000000. Когда мы подставим в выражение единицу, на выходе получим единицу. Теперь пойдем в обратную сторону, ближе к нулю. Когда мы подставляем в выражение для y ½, она попадает в нижнюю часть дроби. Как мы помним, когда мы делим что-то на дробь, нам нужно умножить на перевернутую эту дробь. Значит, мы получим 2. Очевидно, чем ближе мы к нулю, тем сильнее уходим вверх — подставив 1/1000000, мы получим у = 1000000. Похожая ситуация при подходе слева, но с отрицательным знаком.

То, что происходит в нуле, называется разрывом (по виду графика хорошо понятно почему). В анализе принято классифицировать точки разрыва особым образом. То, что мы сейчас видели, называется точкой разрыва второго рода, поскольку односторонние пределы с двух сторон бесконечны (достаточно того, что один из них бесконечен). Если же односторонние пределы в точке разрыва конечны, то такая точка называется точкой разрыва первого рода.

Длина кривой

С самого начала людям хотелось описывать не только сами объекты, но и их свойства. И раз уж мы говорим о «длине, лишенной ширины», хотелось бы уметь эту длину считать. Мы хорошо умеем считать длины прямых отрезков при помощи линейки, которая позволяет нам определять расстояние между двумя точками, но когда дело касается кривых линий, нам нужен иной метод.

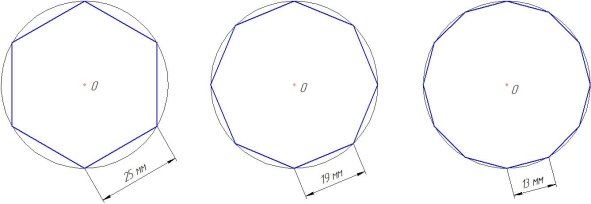
Мы расставляем n точек на равном расстоянии вдоль кривой, после чего замеряем длину прямых отрезков между этими точками (это мы делать умеем). Интуитивно возникает подозрение, что с увеличением числа n мы будем приближаться к значению настоящей длины — прирост суммы будет всё меньше, сверху он ограничен настоящей длинной кривой.

Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.

Гладкость

Еще одним свойством, характеризующим кривые, является гладкость. Хотя смысл слова интуитивно понятен, задать ее математически не совсем элементарно. Мы хотим, чтобы у кривой не было углов, заострений, клювов и т. п.

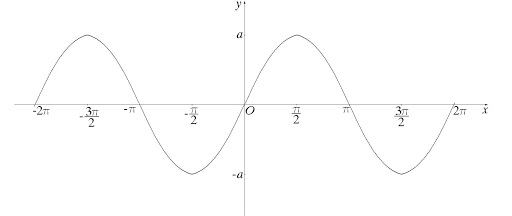
Хороший пример гладкой кривой — синусоида:

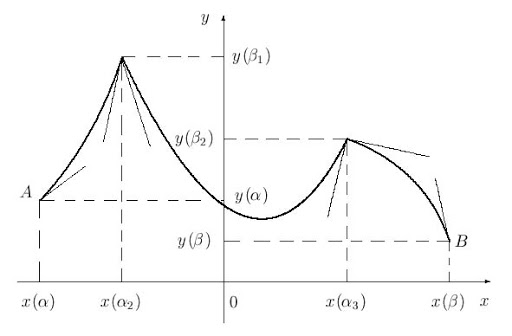
А вот пример негладкой кривой:

Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.

В курсе начал анализа доказывается, что такая касательная неразрывно связана с производной функции, график которой образует нашу кривую: более конкретно — тангенс угла наклона касательной (по отношению к положительному направлению оси Ox) равен значению производной функции в точке касания.

Может быть интересно

Кажется, что гладкость — довольно естественное требование к кривой. Это ощущение привело к тому, что в 1806 году Андре-Мари Ампер выдвинул гипотезу о том, что любая функция всюду, за исключением отдельных, «исключительных и изолированных» точек, имеет производную в этих точках.

Позднее гипотеза была разрушена. Первый контрпример следует атрибутировать, по-видимому, Бернхарду Риману. Более простой и широко известный контрпример был построен Ван дер Варденом позднее, в 1930 году. Но наибольшей известностью пользуется функция Вейерштрасса, выраженная формулой:

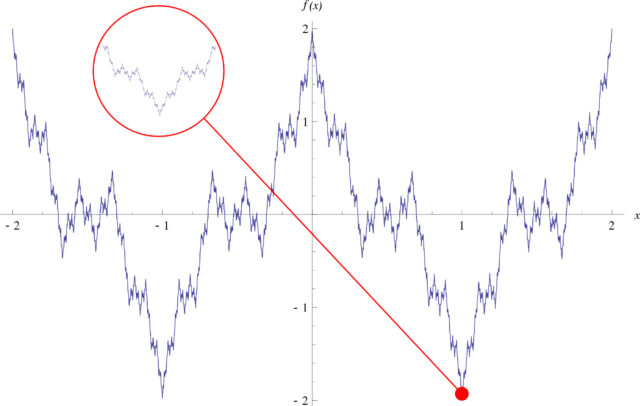
здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой:

Бесконечность в глубине отрезка

Совсем другой подход к кривым предложил великий французский математик Мари Энмон Камиль Жордан. Что если мы возьмем все точки отрезка и с помощью некоторого отображения перенесем их в пространство? Представьте, что наш отрезок сделан из проволоки, которую можно гнуть, вытягивать и сжимать. С помощью сжатия и вытягивания мы можем добиться изменения длины нашего отрезка, а с помощью сгибания — изменения его формы. Если же строго, то жордановой дугой называется образ непрерывного вложения отрезка в пространство: то есть разные точки отрезка обязательно перейдут в разные точки кривой. Можно представить, что отрезок у нас — временной, скажем, от начала работы секундомера до конца его работы. Тогда каждую секунду мы переводим в какое-то положение точки.

Жордановой замкнутой кривой называют образ непрерывного вложения окружности в пространство (из накладываемых требований следует, что окружность обязательно перейдет в некоторую замкнутую линию).

И хотя концепт жордановой кривой кажется достаточно простым, с его помощью можно получить весьма парадоксальные результаты.

В 1903 году Уильям Фогг Осгуд рассмотрел кривую, которая, являясь жордановой кривой, заполняет собой квадрат и в некоторых своих частях (более строго — порциях) имеет ненулевую площадь.

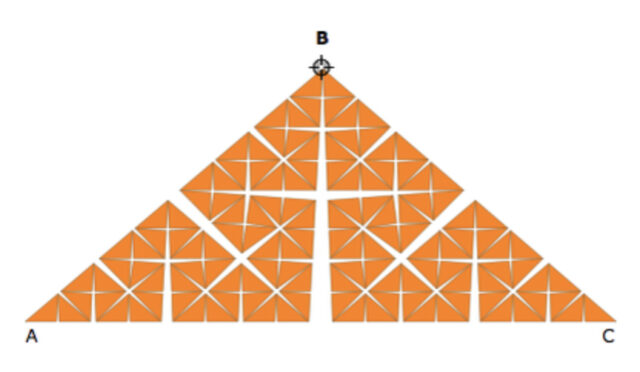
Впоследствии Кнопп построил жорданову кривую, обладающую ненулевой площадью вдоль всей кривой. Этот результат достигается за счет очень узких вырезаемых «клиньев», узость которых приводит к тому, что вычитаемая из площади треугольника площадь падает экспоненциально.

Кстати, вот здесь можно построить ее самостоятельно.

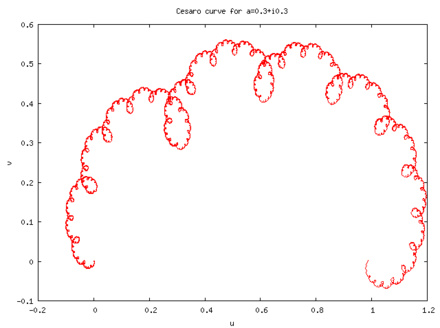
Примеров на эту тему много. Здесь мы упомянем полученные аффинными преобразованиями кривые де Рама:

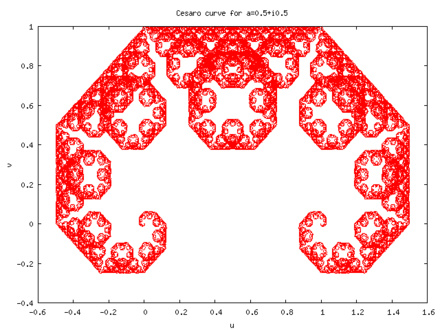
кривую Коха — Пеано

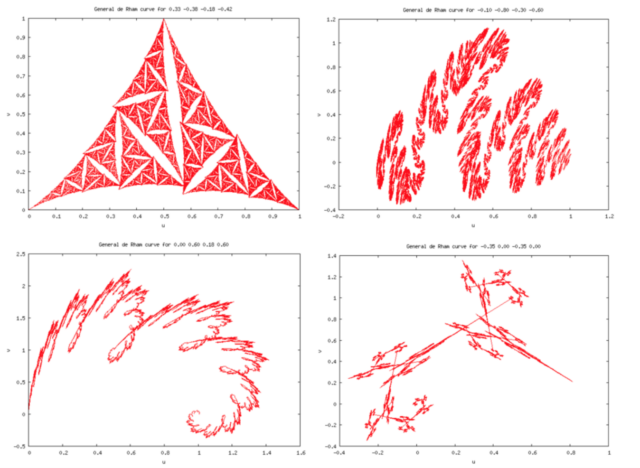
и еще несколько кривых де Рама:

Заполнить плоскость

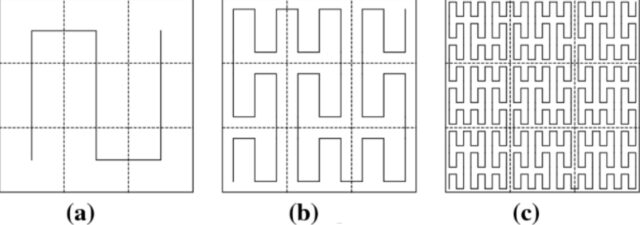
В 1890 году итальянский математик Джузеппе Пеано построил непрерывную кривую, которая проходит через любую точку квадрата (в оригинале использовался единичный, но построение легко повторить для квадрата любых размеров). Пеано задавался вопросом: может ли кривая заполнить всю плоскость или пространство? Результат Пеано воспринимался контринтуитивно. Годом позже кривую с тем же свойством построил уже графически Давид Гильберт.

В дальнейшем все кривые со свойством «заполнения» квадрата стали называть кривыми Пеано, а в более узком смысле это название закрепилось за конкретной кривой из его статьи 1890 года. Поскольку кривая заполняет любой наперед заданный квадрат, мы можем использовать ее и для заполнения плоскости, а в более общем случае — пространства или пустоты внутри нас.

Здесь нужно сделать важное уточнение — отображение с отрезка на квадрат, построенное Пеано, не взаимно-однозначно: не существует кривых Пеано, в которых каждая точка квадрата проходится только единожды — везде при этом построении возникают кратные точки.

Однако существуют кривые Пеано, у которых каждая точка проходится не более трех раз (и множество таких точек счетно).

Интересный факт следует из наших построений. Можно задать параметрически пространственную дугу, которая при проецировании на горизонтальную плоскость будет давать сплошное пятно; при этом такая «крыша» будет давать тень от вертикальных лучей света, но не спасет от дождя, поскольку ее поверхность получается не сплошной.

Ни одна кривая Пеано не гладкая. На интуитивном уровне можно объяснить это необходимостью очень быстро разворачивать направление нашей кривой, что невозможно сделать гладко. Сам Пеано в первой работе на эту тему сознательно не приводил построение кривой, чтобы не опираться на рисунок, однако мы всё же приведем это построение:

Обратите внимание на клетки, они позволяют понять, что происходит на каждом участке. То, что получится в результате бесконечного процесса этого рода, и называется кривой Пеано.

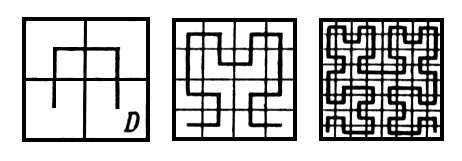
Обладающую тем же свойством кривую построил и современник Пеано Гильберт. Его кривая строится следующим образом:

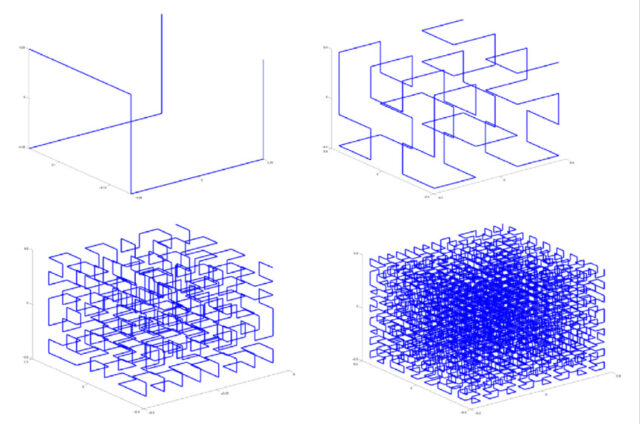
Существуют и объемные, и многомерные аналоги кривой Пеано, заполняющие куб (многомерный куб, соответственно).

Приведем несколько примеров других кривых, обладающих этим свойством.

Фракталы

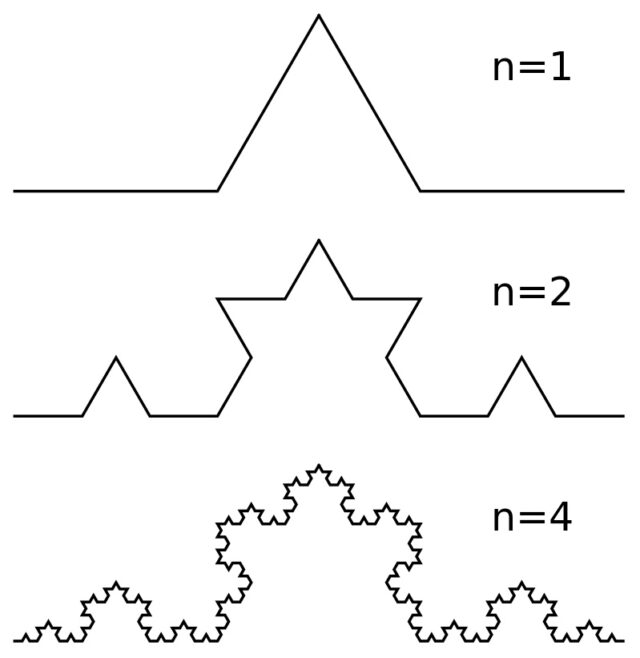
Подробнее об этом виде кривых мы писали тут. Однако в рамках разговора об эволюции представлений о кривых не упомянуть их невозможно. Классическим примером фрактала (фигуры со свойством самоподобия) является кривая Коха.

Свойство самоподобия означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:

В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.

Читайте также

Наш подход с прямыми отрезками терпит здесь фиаско — вместо приближения к какой-то конечной длине сумма длин отрезков неограниченно растет.

Конечно, кривые, обладающие этим свойством, не исчерпываются самоподобными фигурами. Достаточно найти трещину на стене не самой простой формы: самоподобия в ней мы, как правило, не наблюдаем, и в то же время от одной ее «ветки» отходят новые, иной формы, и т. д.

Интересно, что тотально (то есть на любой порции) неспрямляемая кривая очень плохо помещается в ту же концепцию кривой как траектории движения. Точка, движущаяся по такой траектории, очевидно движется не по законам классической механики.

Во-первых, если бы точка двигалась с конечной скоростью по такой кривой, то она бы не двигалась вовсе: сколь угодно малая дуга здесь имеет бесконечную дугу. Но более того — такая кривая нигде не имеет и касательной, а значит, и направление скорости не задано!

В этом кратком обзоре мы лишь немного коснулись трансформации интуитивного представления о кривой в анализе — оставив за скобками развитие этого понятия в алгебре или современной геометрии, равно как и все вопросы, связанные с исследованием строения кривых.

Если эти — опущенные здесь — вопросы заинтересовали вас, то рекомендуем обратиться, например, к популярной брошюре В. И. Арнольда «Вещественная алгебраическая геометрия», а также к брошюре В. В. Острика и М. А. Цфасмана «Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые».

Источник