Топология для чего нужна

Введение в топологию (для чайников и гуманитариев)

Не помню, когда я впервые узнал про топологию, но меня эта наука сразу заинтересовала. Чайник превращается в бублик, сфера выворачивается наизнанку. Многие слышали про это. Но у тех, кто хочет углубиться в эту тему на более серьёзном уровне, часто возникают трудности. Особенно это относится к освоению самых начальных понятий, которые по своей сути очень абстрактны. Более того, многие источники, как будто специально стремятся запутать читателя. Скажем русская вики даёт весьма туманную формулировку того, чем занимается топология. Там говорится, что это наука изучающая топологические пространства. В статье про топологические пространства читатель может узнать, что топологические пространства — это пространства снабжённые топологией. Такие объяснения в стиле лемовских сепулек не очень проясняют суть предмета. Я попробую далее изложить основные базовые понятия в более ясной форме. В моей заметке не будет превращающихся чайников и бубликов, но будут сделаны первые шаги, которые позволят в конце концов научиться этой магии.

Впрочем, так как я не математик, а стопроцентный гуманитарий, то вполне возможно, что написанное ниже — враньё! Ну, или по крайней мере часть.

Впервые я написал эту заметку, как начало цикла статей о топологии, для своих гуманитарных друзей, но никто из них читать ее не стал. Исправленную и расширенную версию я решил выложить на хабр. Мне показалось, что здесь существует определенный интерес к этой теме и статей как раз такого рода еще не было. Заранее благодарен за все комментарии об ошибках и неточностях. Предупреждаю, что я использую много картинок.

Начнем с краткого повторения теории множеств. Думаю, большинство читателей хорошо с ней знакомы, но тем не менее напомню основы.

Итак, считается, что определения у множества нет и, что мы интуитивно понимаем, что это такое. Кантор говорил так: «Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)». Конечно, это просто иносказательное описание, а не математическое определение.
Теория множеств известна (прошу простить за каламбур) множеством удивительных парадоксов. Например. С ней также связан кризис математики в начале XX-го века.

Теория множеств существует в нескольких вариантах, таких как ZFC или NBG и других. Вариантом теории являетсятеория типов, которая весьма важна для программистов. Наконец, некоторые математики предлагает вместо теории множеств в качестве фундамента математики использовать теорию категорий, о которой много написано на Хабре. Теория типов и теория множеств описывают математические объекты как бы «изнутри», а теория категорий не интересуется их внутренним строением, а только как они взаимодействуют, т.е. даёт их «внешнюю» характеристику.
Для нас важны только самые начальные основы теории множеств.

Множества бывают конечными.

Бывают бесконечными. Например, множество целых чисел, которое обозначается буквой ℤ (или просто Z, если у вас на клавиатуре нет фигурных букв).

Наконец, есть пустое множество. Оно ровно одно во всей Вселенной. Имеется простое доказательство этого факта, но я не буду его здесь приводить.

Если множество бесконечно, оно бывает счетным. Счетные — те множества, элементы которых можно перенумеровать натуральными числами. Само множество натуральных чисел, как вы догадались, тоже счетно. А вот как можно пронумеровать целые числа.

С рациональными числами сложнее, но и они поддаются нумерации. Этот способ называется диагональным процессом и выглядит, как на картинке внизу.

Обобщением понятия размера для множеств является мощность. Мощность конечных множеств равна числу их элементов. Мощность бесконечных множеств обозначается еврейской буквой алеф с индексом. Самая маленькая бесконечная мощность—это мощность ℵ₀. Она равна мощности счетных множеств. Как видим, таким образом, натуральных чисел, так же много, как и целых или рациональных. Странно, но факт. Следующая — мощность континуума. Она обозначается маленькой готической буквой с. Это мощность множества вещественных чисел ℝ, например. Существует гипотеза о том, что мощность континуума равна мощности ℵ₁. Т.е., что это следующая после мощности счетных множеств мощность, и нет никакой промежуточной мощности между счетными множествами и континуумом.

Над множествами можно проводить различные операции и получать новые множества.

1. Множества можно объединять.

2. Множества можно «вычитать». Эта операция называется дополнением.

3. Можно искать пересечение множеств.

Собственно это все о множествах, что нужно знать для целей этой заметки. Теперь мы можем приступить к самой топологии.
Топология — это наука, которая изучает множества с определенной структурой. Эта структура также называется топологией.
Пусть у нас есть некоторое непустое множество S.
Пусть же у этого множества будет некоторая структура, которая описывается с помощью множества, которое мы назовем Т. Т представляет собой множество подмножеств множества S такое, что:

1. Само S и ∅ принадлежат T.
2. Любое объединение произвольных семейств элементов T принадлежит T.
3. Пересечение произвольного конечного семейства элементов T принадлежит T.

Если эти три пункта выполняются, то наша структура является топологией T на множестве S. Элементы множества T называются открытыми множествами на S в топологии T. Дополнением к открытым множествам являются замкнутые множества. Важно отметить, что если множество открыто, это еще не означает, что оно не замкнуто и наоборот. Кроме того в данном множестве относительно некоторой топологии могут быть подмножества, которые не являются ни открытыми, ни замкнутыми.

Приведем пример. Пусть у нас есть множество, состоящее из трех цветных треугольников.

Самая простая топология на нем называется антидискретной топологией. Вот она.

Эту топологию, также называют топологией слипшихся точек. Она состоит из самого множества и из пустого множества. Это действительно удовлетворяет аксиомам топологии.

На одном множестве можно задать несколько топологий. Вот еще одна очень примитивная топология, которая бывает. Она называется дискретной. Это топология, которая состоит из всех подмножеств данного множества.

А вот еще топология. Она задана на множестве из 7 разноцветных звезд S, которые я обозначил буквами. Убедитесь, что это топология. Я в этом не уверен, вдруг я пропустил, какое-то объединение или пересечение. На этой картинке должно быть само множество S, пустое множество, пересечения и объединения всех остальных элементов топологии также должны быть на картинке.

Пара из топологии и множества на котором она задана называется топологическим пространством.

Если в множестве много точек (не говоря уже о том, что их может быть бесконечно много ), то перечислить все открытые множества может быть проблематично. Например, для дискретной топологии на множестве из трех элементов, надо составить список из 8 множеств. А для 4-элементного множества дискретная топология будет насчитывать уже 16, для 5 — 32, для 6 —64 и так далее. Для того, чтобы не перечислять все открытые множества используется как бы сокращенная запись — выписываются те элементы, объединения которых могут дать, все открытые множества. Это называется базой топологии. Например, для дискретной топологии пространства из трех треугольников — это будут три треугольника взятые в отдельности, потому, что объединяя их, можно получить все остальные открытые множества в данной топологии. Говорят, что база генерирует топологию. Множества, элементы которого генерируют базу, называют предбазой.

Ниже пример базы для дискретной топологии на множестве из пяти звезд. Как видите, в данном случае база состоит всего из пяти элементов, в то время как в топологии целых 32 подмножества. Согласитесь, использовать базу для описания топологии — гораздо удобнее.

Для чего нужны открытые множества? В каком-то смысле они дают представление о «близости» между точками и о различии между ними. Если точки принадлежат двум разным открытым множествам или если одна точка находится в открытом множестве, в котором не находится вторая, то они топологически различаются. В антидискретной топологии все точки в этом смысле неразличимы, они как бы слиплись. Наоборот, в дискретной топологии все точки имеют различие.

С понятием открытого множества неразрывно связано понятие окрестности. Некоторые авторы дают определение топологии не через открытые множества, а через окрестности. Окрестность точки p — это множество, которое содержит открытый шар с центром в этой точке. Например, на рисунке ниже показаны окрестности и не окрестности точек. Множество S₁ является окрестностью точки p, а множество S₂ нет.

Связь между открытым множеством и октестностью можно сформулировать так. Открытое множество — такое множество, каждый элемент которого имеет некоторую окрестность, лежащую в данном множестве. Или наоборот можно сказать, что множество открыто, если оно является окрестностью любой своей точки.

Все это самые базовые понятия топологии. Отсюда еще не ясно как выворачивать сферы наизнанку. Возможно в будущем, я смогу добраться и до такого рода тем (если сам разберусь).

UPD. Из-за неаккуратности моей речи, возникло некоторое недоумение относительно мощностей множеств. Я несколько исправил свой текст и здесь хочу дать пояснение. Кантор, создавая свою теорию множеств, ввел понятие мощности, которое позволяло сравнивать бесконечные множества. Кантор установил, что мощности счетных множеств (например, рациональных чисел) и континуума (например, вещественных чисел) различны. Он предположил, что мощность континуума является следующей после мощности счетных множеств т.е. равна алеф-один. Кантор пытался доказать эту гипотезу, но безуспешно. Позже стало ясно, что эту гипотезу нельзя ни опровергнуть, ни доказать.

Источник

Топология

часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.

I. Общая топология

Часть Т., ориентированная на аксиоматическое изучение непрерывности, называется общей Т. Наряду с алгеброй общая Т. составляет основу современного теоретико-множественного метода в математике.

Аксиоматически непрерывность можно определить многими (вообще говоря, неравносильными) способами. Общепринята аксиоматика, основывающаяся на понятии открытого множества. Топологической структурой, или топологией, на множестве Х называют такое семейство его подмножеств, называемых открытыми множествами, что: 1) пустое множество ∅ и всё Х открыты; 2) объединение любого числа и пересечение конечного числа открытых множеств открыто. Множество, на котором задана топологическая структура, называют топологическим пространством (См. Топологическое пространство). В топологическом пространстве Х можно определить все основные понятия элементарного анализа, связанные с непрерывностью. Например, окрестностью точки x ∈ X называют произвольное открытое множество, содержащее эту точку; множество A ⊂ X называют замкнутым, если его дополнение Х А открыто; замыканием множества А называют наименьшее замкнутое множество, содержащее A; если это замыкание совпадает с X, то А называют всюду плотным в Х и т.д.

По определению, ∅ и Х являются одновременно замкнутыми и открытыми множествами. Если в Х нет других множеств, одновременно замкнутых и открытых, то топологическое пространство Х называют связным. Наглядно связное пространство состоит из одного «куска», а несвязное — из нескольких.

Любое подмножество А топологического пространства Х обладает естественной топологической структурой, состоящей из пересечений с А открытых множеств из X. Снабженное этой структурой А называют подпространством пространства X. Каждое Метрическое пространство становится топологическим, если за его открытые множества принять множества, содержащие вместе с произвольной точкой некоторую её ε-окрестность (шар радиуса ε с центром в этой точке). В частности, любое подмножество n-мерного евклидова пространства 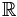n является топологическим пространством. Теория таких пространств (под названием «геометрической Т.») и теория метрических пространств включаются по традиции в общую Т.

Открытым покрытием топологического пространства Х называют семейство его открытых множеств, объединением которого является всё X. Топологическое пространство Х называют компактным (в другой терминологии —бикомпактным), если любое его открытое покрытие содержит конечное число элементов, также образующих покрытие. Классическая теорема Гейне — Бореля утверждает, что любое ограниченное замкнутое подмножество 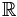n компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Т., имеющих общематематическое значение.

Открытое покрытие <V_β> называют вписанным в покрытие <U_α>, если для любого β существует α такое, что V_β ⊂ U_α. Покрытие <V_β> называют локально конечным, если каждая точка х ∈ Х обладает окрестностью, пересекающейся только с конечным числом элементов этого покрытия. Топологическое пространство называют паракомпактным, если в любое его открытое покрытие можно вписать локально конечное покрытие. Класс паракомпактных пространств является примером классов топологических пространств, получающихся наложением так называемых условий типа компактности. Этот класс очень широк, в частности он содержит все метризуемые топологические пространства, то есть пространства X, в которых можно ввести такую метрику ρ, что Т., порожденная ρ в X, совпадает с Т., заданной в X.

Кратностью открытого покрытия называют наибольшее число k такое, что найдётся k его элементов, имеющих непустое пересечение. Наименьшее число n, обладающее тем свойством, что в любое конечное открытое покрытие топологического пространства Х можно вписать открытое покрытие кратности ≤n + 1, обозначается символом dimХ и называется размерностью X. Это название оправдано тем, что в элементарно-геометрических ситуациях dimХ совпадает с обычно понимаемой размерностью, например dim 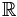n = n. Возможны и др. числовые функции топологического пространства X, отличающиеся от dimX, но в простейших случаях совпадающие с dimX. Их изучение составляет предмет общей теории размерности — наиболее геометрически ориентированной части общей Т. Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.

Важные классы топологических пространств получаются наложением так называемых аксиом отделимости. Примером является так называемая аксиома Хаусдорфа, или аксиома T₂, требующая, чтобы любые две различные точки обладали непересекающимися окрестностями. Топологическое пространство, удовлетворяющее этой аксиоме, называется хаусдорфовым, или отделимым. Некоторое время в математической практике встречались почти исключительно хаусдорфовы пространства (например, любое метрическое пространство хаусдорфово). Однако роль нехаусдорфовых топологических пространств в анализе и геометрии постоянно растет.

Топологические пространства, являющиеся подпространствами хаусдорфовых (би) компактных пространств, называются вполне регулярными или тихоновскими. Их тоже можно охарактеризовать некоторой аксиомой отделимости, а именно: аксиомой, требующей, чтобы для любой точки x₀ ∈ Х и любого не содержащего её замкнутого множества F 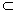Х существовала непрерывная функция g : Х → [0, 1], равная нулю в x₀ и единице на F.

Топологические пространства, являющиеся открытыми подпространствами хаусдорфовых компактных, называются локально компактными пространствами. Они характеризуются (в классе хаусдорфовых пространств) тем, что каждая их точка обладает окрестностью с компактным замыканием (пример: евклидово пространство). Любое такое пространство дополняется одной точкой до компактного (пример: присоединением одной точки из плоскости получается сфера комплексного переменного, а из n — сфера S n ).

Отображение f : X → Y топологическое пространства Х в топологическое пространство Y называют непрерывным отображением, если для любого открытого множества V ⊂ Y множество f —1 (V) открыто в X. Непрерывное отображение называют гомеоморфизмом, если оно взаимно однозначно и обратное отображение f —1 : Y → X непрерывно. Такое отображение устанавливает взаимно однозначное соответствие между открытыми множествами топологических пространств Х и Y, перестановочное с операциями объединения и пересечения множеств. Поэтому все топологические свойства (то есть свойства, формулируемые в терминах открытых множеств) этих пространств одни и те же, и с топологической точки зрения гомеоморфные топологические пространства (то есть пространства, для которых существует хотя бы один гомеоморфизм Х → Y) следует считать одинаковыми (подобно тому как в евклидовой геометрии одинаковыми считаются фигуры, которые можно совместить движением). Например, гомеоморфны («топологически одинаковы») окружность и граница квадрата, шестиугольника и т.п. Вообще любые две простые (не имеющие двойных точек) замкнутые линии гомеоморфны. Напротив, окружность не гомеоморфна прямой (ибо удаление точки не нарушает связности окружности, но нарушает связность прямой; по той же причине прямая не гомеоморфна плоскости, а окружность не гомеоморфна «восьмёрке»). Окружность не гомеоморфна также и плоскости (выкиньте не одну, а две точки).

Если Х — топологическое пространство, а Y — произвольное множество и если задано отображение p : X → Y пространства Х на множество Y (например, если Y является фактормножеством Х по некоторому отношению эквивалентности, а p представляет собой естественную проекцию, сопоставляющую с каждым элементом х ∈ Х его класс эквивалентности), то можно ставить вопрос о введении в Y топологической структуры, относительно которой отображение p непрерывно. Наиболее «богатую» (открытыми множествами) такую структуру получают, полагая открытыми множествами в Y все те множества V ⊂ Y, для которых множество f ‑1 (V) ⊂ Х открыто в X. Снабженное этой топологической структурой множество Y называется факторпространством топологического пространства Х (по отношению к p ). Оно обладает тем свойством, что произвольное отображение f : Y → Z тогда и только тогда непрерывно, когда непрерывно отображение 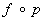: X → Z. Непрерывное отображение p : X → Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X. Непрерывное отображение p : X → Y называется открытым, если для любого открытого множества U ⊂ Х множество p(U) открыто в Y, и замкнутым, если для любого замкнутого множества F ⊂ Х множество p(F) замкнуто в Y. Как открытые, так и замкнутые непрерывные отображения f : Х → Y, для которых f(X) = Y, являются факторными.

Пусть Х — топологическое пространство, А — его подпространство и f : A → Y — непрерывное отображение. Предполагая топологические пространства Х и Y непересекающимися, введём в их объединении Х ∪ Y топологическую структуру, считая открытыми множествами объединения открытых множеств из Х и Y. Далее, введём в пространстве Х ∪ Y наименьшее отношение эквивалентности, в котором a

f(α) для любой точки a ∈ А. Соответствующее факторпространство обозначается символом X ∪ _fY, и о нём говорят, что оно получено приклеиванием топологического пространства Х к топологическому пространству Y по А посредством непрерывного отображения f. Эта простая и наглядная операция оказывается очень важной, так как позволяет получать из сравнительно простых топологических пространств более сложные. Если Y состоит из одной точки, то пространство Х ∪ _fY обозначается символом Х/А и о нём говорят, что оно получено из Х стягиванием А в точку. Например, если Х — диск, а А — его граничная окружность, то Х/А гомеоморфно сфере.

2. Равномерная топология

Часть Т., изучающая аксиоматическое понятие равномерной непрерывности, называется равномерной Т. Известное из анализа определение равномерной непрерывности числовых функций непосредственно переносится на отображения любых метрических пространств. Поэтому аксиоматику равномерной непрерывности обычно получают, отталкиваясь от метрических пространств. Подробно исследованы два аксиоматических подхода к равномерной непрерывности, основанных соответственно на понятиях близости и окружения диагонали.

Источник

ТОПОЛОГИЯ

Полезное

Смотреть что такое «ТОПОЛОГИЯ» в других словарях:

топология — топология … Орфографический словарь-справочник

топология — Физическое или логическое распределение узлов сети. Физическая топология определяет физические связи (каналы) между узлами. Логическая топология описывает возможные соединения между сетевыми узлами. В локальных сетях наиболее распространены три… … Справочник технического переводчика

ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия

ТОПОЛОГИЯ — ТОПОЛОГИЯ, раздел математики, изучающий свойства геометрических фигур, остающиеся неизменными при любой деформации сдавливании, растягивании, скручивании (но без разрывов и склеиваний). Чашка с ручкой топологически эквивалентна бублику; куб,… … Научно-технический энциклопедический словарь

ТОПОЛОГИЯ — ТОПОЛОГИЯ, топологии, мн. нет, жен. (от греч. topos место и logos учение) (мат.). Часть геометрии, исследующая качественные свойства фигур (т.е. не зависящие от таких понятий, как длина, величина углов, прямолинейность и т.п.). Толковый словарь… … Толковый словарь Ушакова

топология — сущ., кол во синонимов: 1 • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Топология — Topology раздел математики, изучающий свойства геометрических фигур, которые не изменяются при деформациях, происходящих без разрывов. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

топология ИС — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN integrated circuit layout … Справочник технического переводчика

Топология — Не следует путать с топографией. У этого термина существуют и другие значения, см. Топология (значения). Лента Мёбиуса поверхно … Википедия

Источник